library(purrr)
library(dplyr)Outbreaks simulations
Implementation of the method described in Noufaily et al. (2013).
Required packages:
A tuning of the dplyr::bind_col() function:
bind_cols2 <- function(...) dplyr::bind_cols(..., .name_repair = "unique_quiet")A tuning of the rpois() function:
rpois2 <- function(lambda) rpois(length(lambda), lambda)A tuning of the plot() function:
plot2 <- function(...) plot(..., type = "s", xlab = "week", ylab = "count")A function that generates the mean of the incidence as a function of time (in weeks) with trend and seasonality:
mu <- function(t, theta, beta, gamma1, gamma2, m) {
t2 <- 2 * pi * t((1:m) %*% t(t)) / 52
exp(theta + beta * t + rowSums(gamma1 * cos(t2) + gamma2 * sin(t2)))
}A function that stochastically generates incidence as a function of time using the mean as generated by the above mu() function and a negative binomial distribution. This is how it should be done if the dispersion parameter \(\phi\) is interpreted correctly:
baseline1 <- function(n, t, theta, beta, gamma1, gamma2, phi, m) {
counts <- mu(t, theta, beta, gamma1, gamma2, m)
1:n |>
map(~ rnbinom(t, phi, mu = counts)) |>
bind_cols2()
}This is how it’s done in the article:
baseline2 <- function(n, t, theta, beta, gamma1, gamma2, phi, m) {
counts <- mu(t, theta, beta, gamma1, gamma2, m)
prob <- 1 / phi
size <- counts * prob / (1 - prob)
1:n |>
map(~ rnbinom(t, size, prob)) |>
bind_cols2()
}A function that generates the standard deviation of the incidence as a function of time, as it should be done if the dispersion parameter \(\phi\) is interpreted correctly:
stddev1 <- function(t, theta, beta, gamma1, gamma2, phi, m) {
counts <- mu(t, theta, beta, gamma1, gamma2, m)
sqrt(counts * (1 + counts / phi))
}As it’s done in the article:
stddev2 <- function(t, theta, beta, gamma1, gamma2, phi, m) {
sqrt(mu(t, theta, beta, gamma1, gamma2, m) * phi)
}A function that simulates outbreak cases to add to non-outbreak cases:
outbreaks_cases <- function(stimes, stddev, indexes, k, weights) {
k * stddev[stimes] |>
rpois2() |>
map2(stimes - 1, ~ c(rep(0, .y), round(.x * weights))[indexes]) |>
bind_cols2() |>
rowSums()
}where stimes is a vector of outbreak starting times, stddev is a vector of the standard deviation of incidence as a function of time, indexes is a vector of indexes of the input time series (basically seq_along(stddev) here), k is the constant used for the rate of the Poisson distribution that determines the size of the outbreak, and weights is a vector of temporal weights used to spread the total number of cases during the outbreak along time. A function that adds outbreak cases to non-outbreak cases, using the above outbreaks_cases() function:
add_outbreak_cases <- function(weeks, stddev, nb, k, weights) {
indexes <- seq_along(stddev)
1:ncol(weeks) |>
map(~ sample(indexes, nb)) |>
bind_cols2() |>
map(outbreaks_cases, stddev, indexes, k, weights) |>
bind_cols2() |>
magrittr::add(weeks)
}where weeks is the time series of non-outbreak cases and nb is the number of outbreaks we wish to add to the time series of incidence. The simulator that puts together all the above functions:
simulator <- function(n = 12 * 52, N = 100,
theta = 1.5, beta = .003, gamma1 = .2, gamma2 = -.4,
phi = 1, m = 1,
baseline_function = baseline1,
stddev_function = stddev1,
baseline_from = 313, baseline_to = 575,
current_from = 576, current_to = NULL,
meanlog = 0, sdlog = .5,
nb_outbreaks_baseline = 4, nb_outbreaks_current = 1, k = 2) {
if (is.null(current_to)) current_to <- n
baseline_indexes <- baseline_from:baseline_to
current_indexes <- current_from:current_to
t_vals <- 1:n
t_weights <- diff(c(0, plnorm(seq_along(t_vals), meanlog, sdlog)))
baseline_vals <- baseline_function(N, t_vals, theta, beta, gamma1, gamma2, phi, m)
stddev_vals <- stddev_function(t_vals, theta, beta, gamma1, gamma2, phi, m)
baseline_weeks <- baseline_vals[baseline_indexes, ]
baseline_stddev <- stddev_vals[baseline_indexes]
current_weeks <- baseline_vals[current_indexes, ]
current_stddev <- stddev_vals[current_indexes]
list(bsln_outbrk = add_outbreak_cases(baseline_weeks, baseline_stddev,
nb_outbreaks_baseline, k, t_weights),
curr_outbrk = add_outbreak_cases(current_weeks, current_stddev,
nb_outbreaks_current, k, t_weights))
}The scenarios of Figure 2:
scenarios <- list(
s8 = list(theta = - 2, beta = 0, gamma1 = .1, gamma2 = .3, phi = 2, m = 1),
s10 = list(theta = - 2, beta = .005, gamma1 = 0, gamma2 = 0, phi = 2, m = 0),
s12 = list(theta = - 2, beta = .005, gamma1 = .1, gamma2 = .3, phi = 2, m = 2),
s17 = list(theta = 1.5, beta = .003, gamma1 = .2, gamma2 = - .4, phi = 1, m = 1))Generating the data for Figure 2:
set.seed(30101976)
t_vals <- 1:(12 * 52)
data_fig2_1 <- scenarios |>
map(~ with(.x, baseline1(n = 1, t = t_vals, theta = theta, beta = beta,
gamma1 = gamma1, gamma2 = gamma2, phi = phi, m = m))) |>
map(unlist)
data_fig2_2 <- scenarios |>
map(~ with(.x, baseline2(n = 1, t = t_vals, theta = theta, beta = beta,
gamma1 = gamma1, gamma2 = gamma2, phi = phi, m = m))) |>
map(unlist)Figure 2 as it should be done:
opar <- par(mfrow = c(2, 2), plt = c(.12, 1, .18, .98))
walk(data_fig2_1, ~ plot2(t_vals, .x))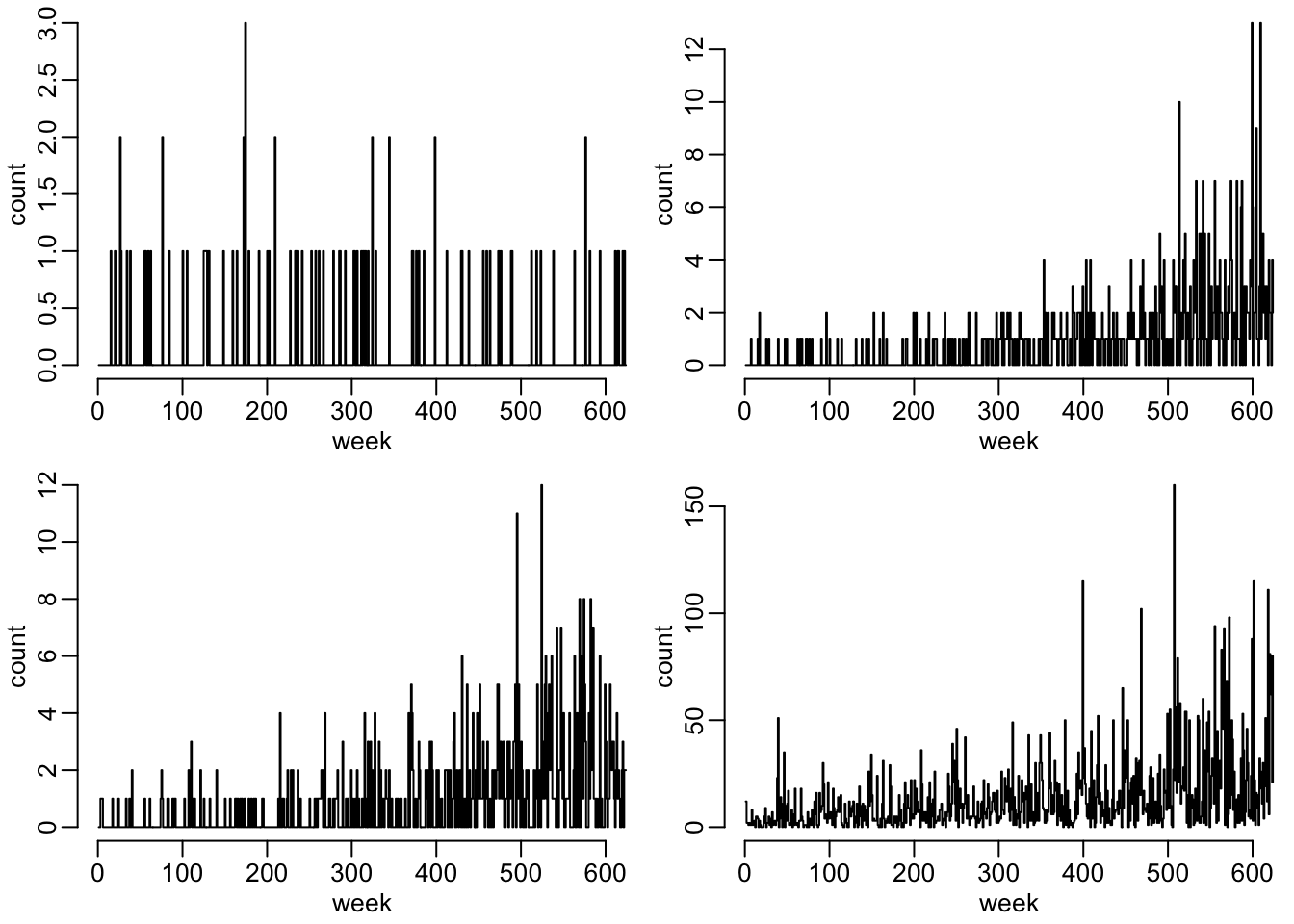
par(opar)Figure 2 as it’s done in the article:
opar <- par(mfrow = c(2, 2), plt = c(.12, 1, .18, .98))
walk(data_fig2_2, ~ plot2(t_vals, .x))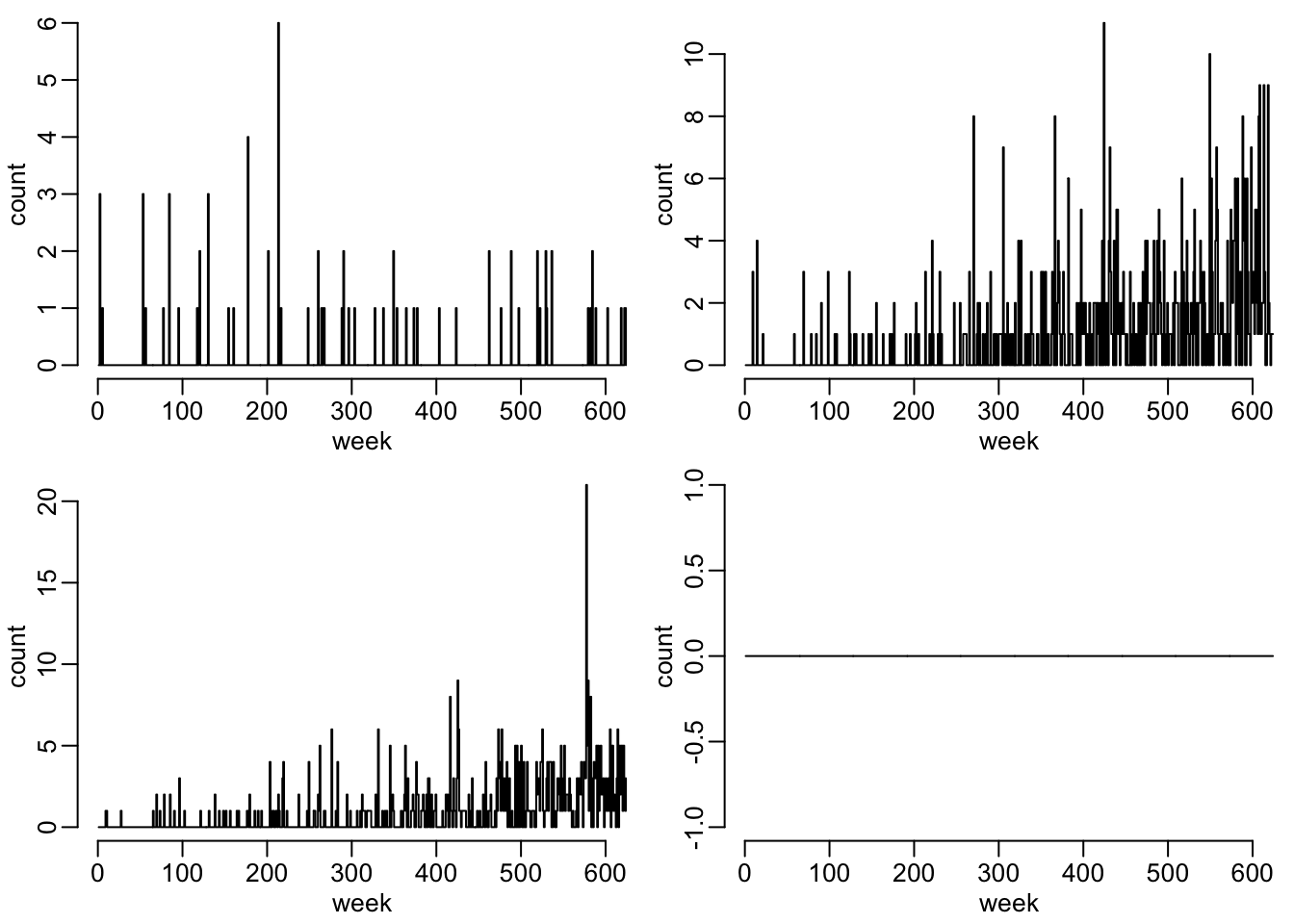
par(opar)There seems to be something wrong with scenario 17… Let’s now run the simulator with the outbreaks for the 4 scenarios and the 2 options regarding the dispersion parameter:
simulations1 <- map(scenarios,
~ with(.x, simulator(theta = theta, beta = beta, gamma1 = gamma1,
gamma2 = gamma2, phi = phi, m = m,
baseline_function = baseline1,
stddev_function = stddev1)))
simulations2 <- map(scenarios,
~ with(.x, simulator(theta = theta, beta = beta, gamma1 = gamma1,
gamma2 = gamma2, phi = phi, m = m,
baseline_function = baseline2,
stddev_function = stddev2)))Values considered for \(k\) is the article: 2, 3, 5 and 10.